排序算法 – Blog website

排序算法

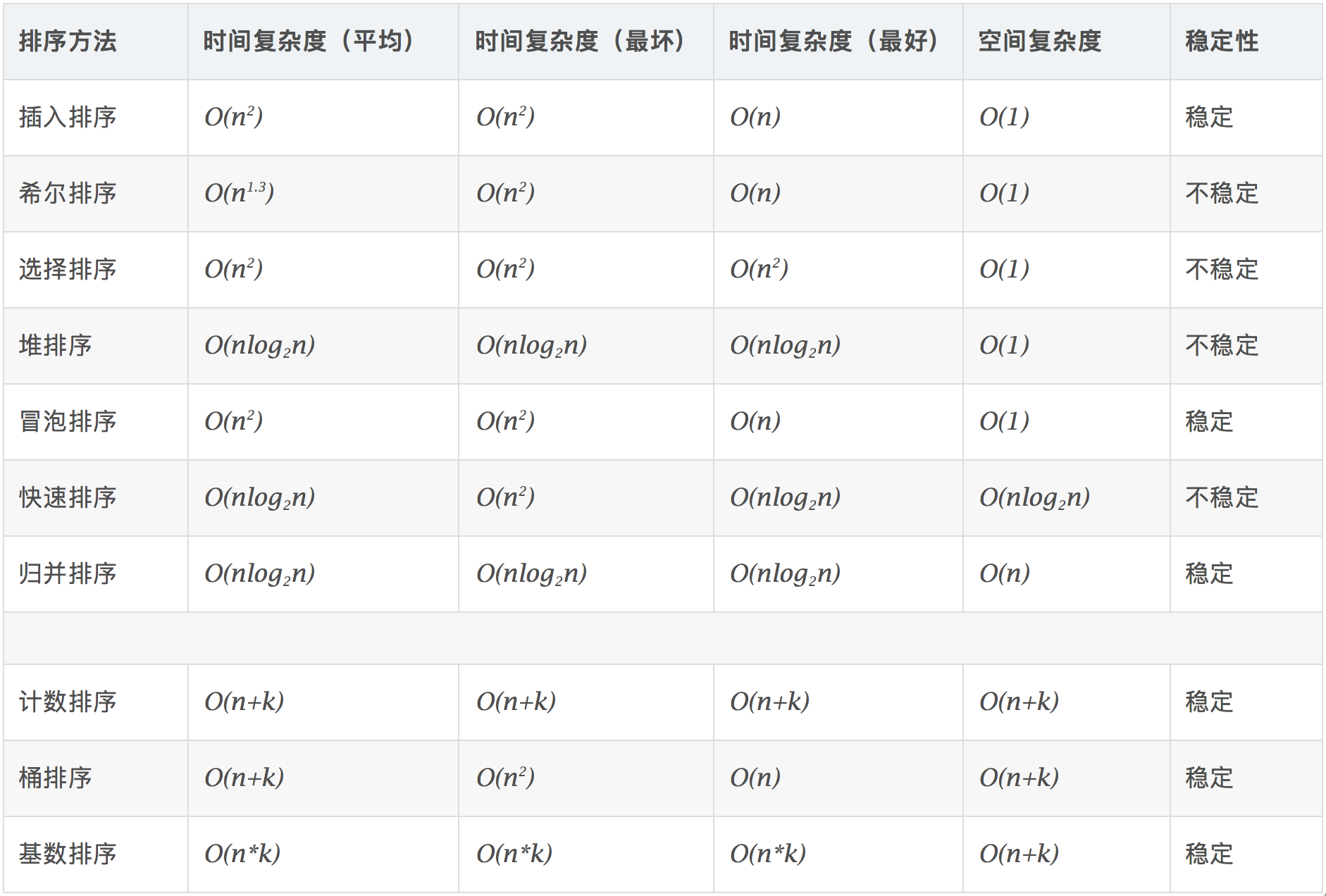
稳定：如果a原本在b前面，而a=b，排序之后a仍然在b的前面。
不稳定：如果a原本在b的前面，而a=b，排序之后 a 可能会出现在 b 的后面。
时间复杂度：对排序数据的总的操作次数。反映当n变化时，操作次数呈现什么规律。
空间复杂度：是指算法在计算机内执行时所需存储空间的度量，它也是数据规模n的函数。

1.冒泡排序

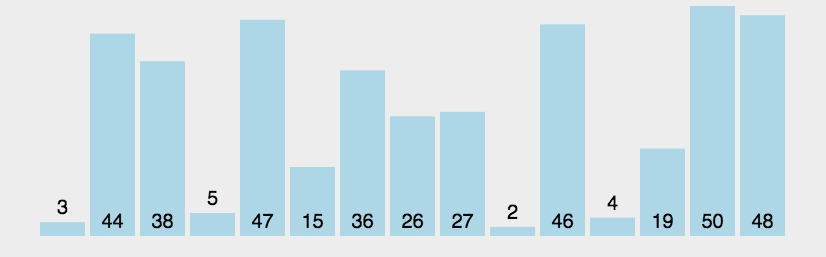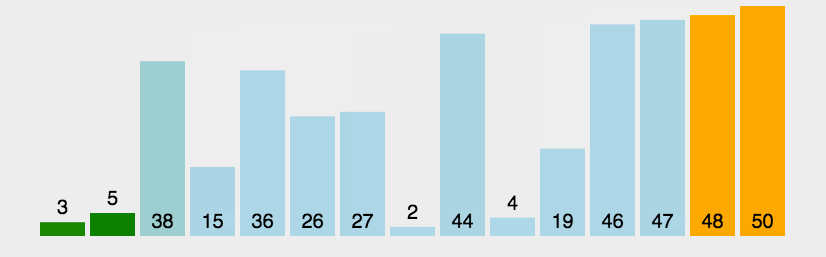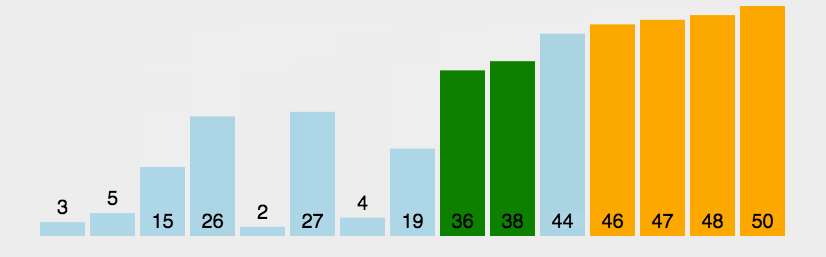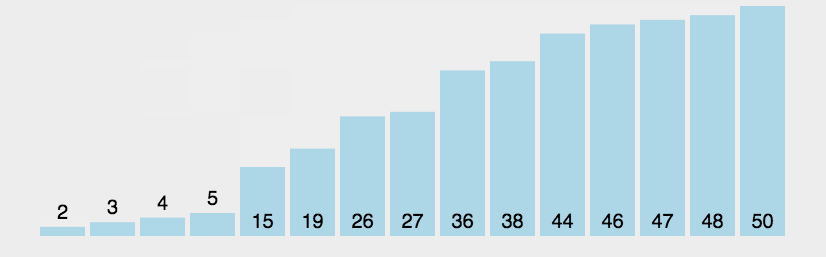
func bubbleSort(arr []int) {
	n := len(arr)
	for i := 0; i < n-1; i++ {
		for j := 0; j < n-1-i; j++ {
			if arr[j] > arr[j+1] {
				arr[j], arr[j+1] = arr[j+1], arr[j]
			}
		}
	}
}

2.插入排序

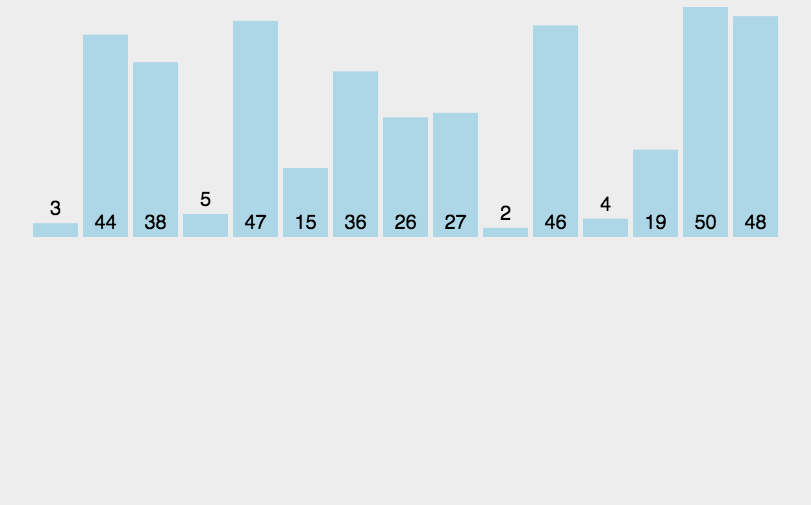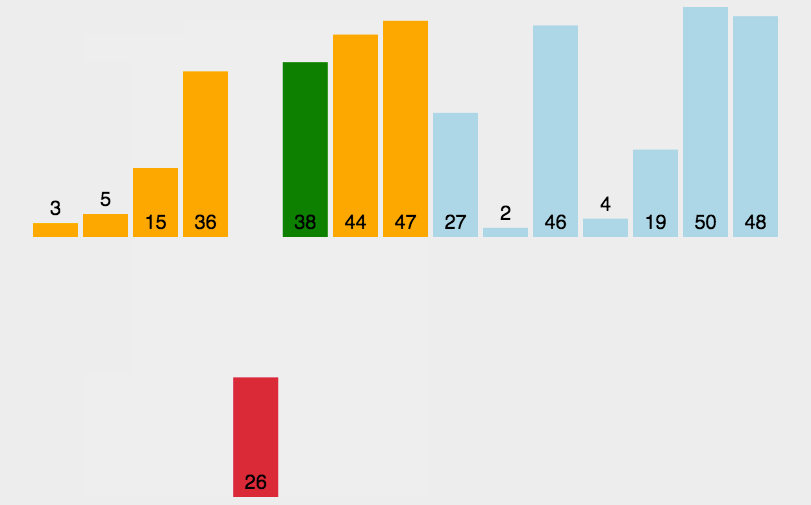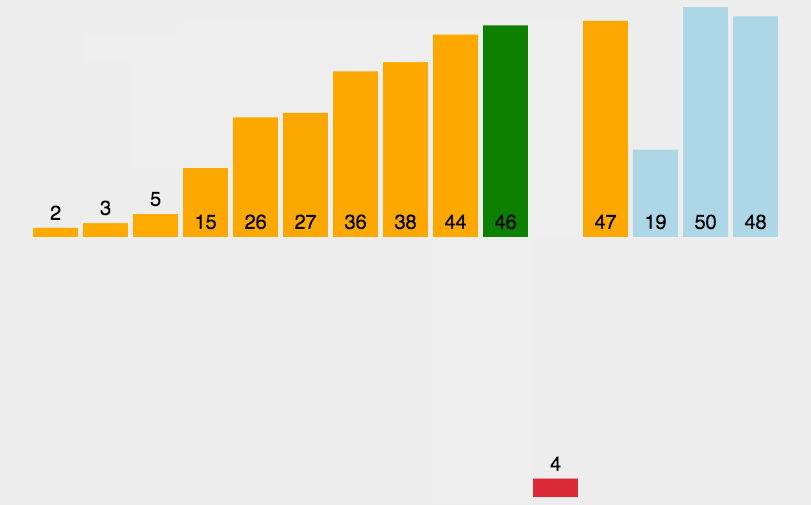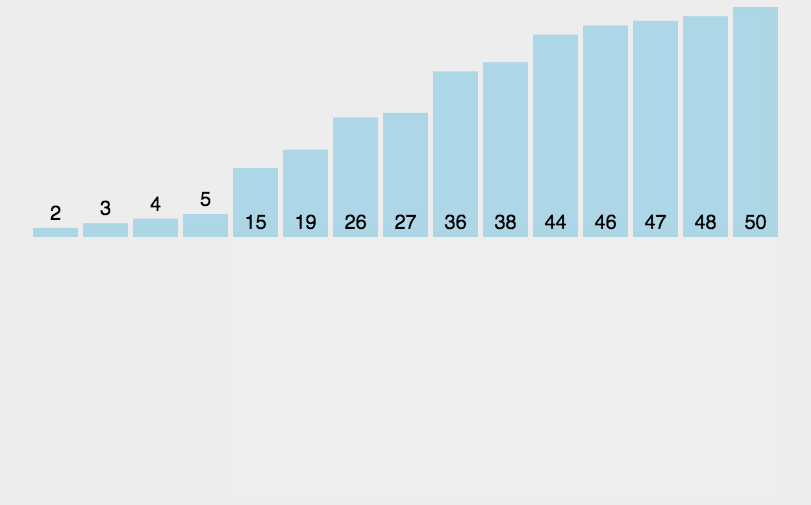
func insertionSort(arr []int) {
	for i := 1; i < len(arr); i++ {
		key := arr[i]
		j := i - 1

		for j >= 0 && arr[j] > key {
			arr[j+1] = arr[j]
			j--
		}
		arr[j+1] = key // 插入动作
	}
}

3.选择排序

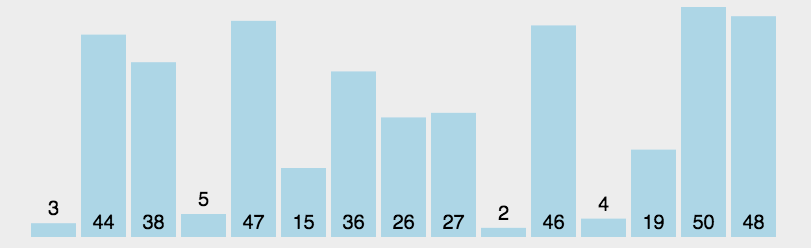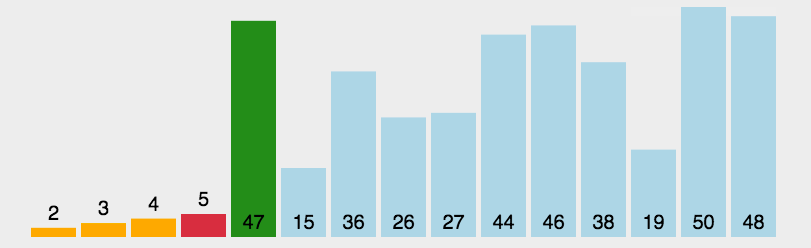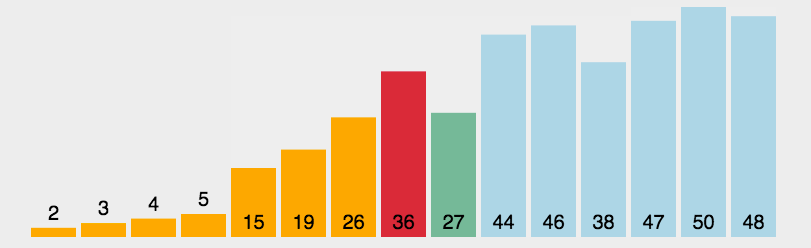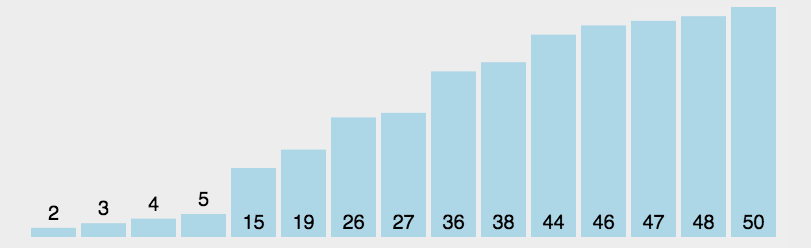
找最小值排序

func selectionSort(arr []int) {
	n := len(arr)
	for i := 0; i < n; i++ {
		minIndex := i
		for j := i; j < n; j++ {
			if arr[j] < arr[minIndex] {
				minIndex = j
			}
		}

		if minIndex != i {
			arr[i], arr[minIndex] = arr[minIndex], arr[i]
		}
	}
}

找最大值排序

func selectionSort(arr []int) {
	for i := len(arr) - 1; i >= 0; i-- {
		maxIndex := i
		for j := i; j >= 0; j-- {
			if arr[j] > arr[maxIndex] {
				maxIndex = j
			}
		}

		if maxIndex != i {
			arr[i], arr[maxIndex] = arr[maxIndex], arr[i]
		}
	}
}

4.快速排序

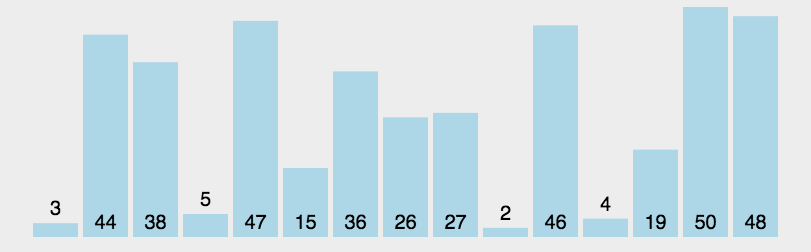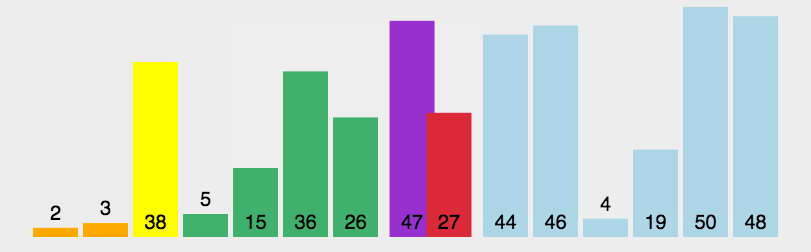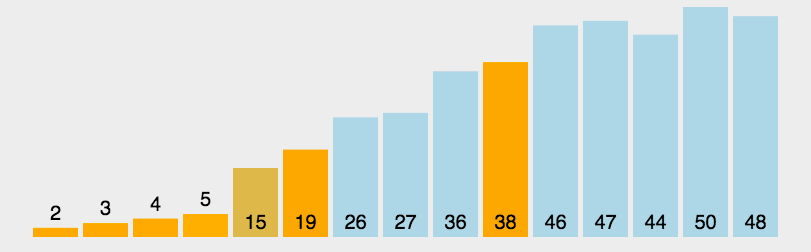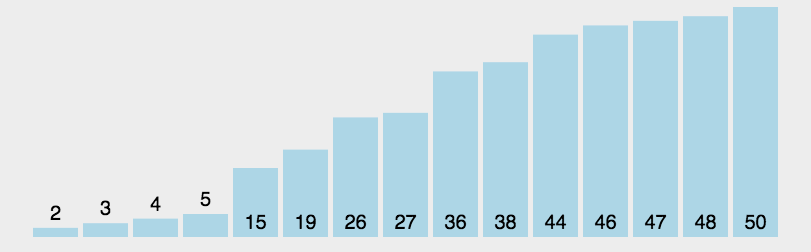
// QuickSort 快速排序函数
func QuickSort(arr []int, low, high int) {
	if low < high {
		pivotIndex := partition(arr, low, high)
		QuickSort(arr, low, pivotIndex-1)  // 递归处理左半部分
		QuickSort(arr, pivotIndex+1, high) // 递归处理右半部分
	}
}

// partition 函数用于对数组进行分区，返回枢轴元素最终所在的位置
func partition(arr []int, low, high int) int {
	pivot := arr[high] // 选取最后一个元素作为枢轴
	i := low - 1       // 设置i指向分割点左侧的位置

	for j := low; j < high; j++ {
		// 查找第一个大于等于枢轴的元素
		if arr[j] <= pivot {
			i++
			arr[i], arr[j] = arr[j], arr[i] // 交换元素，将小于等于枢轴的元素移到左侧
		}
	}

	arr[i+1], arr[high] = arr[high], arr[i+1] // 将枢轴元素放置到最终位置
	return i + 1                              // 返回枢轴元素的索引
}

5.归并排序

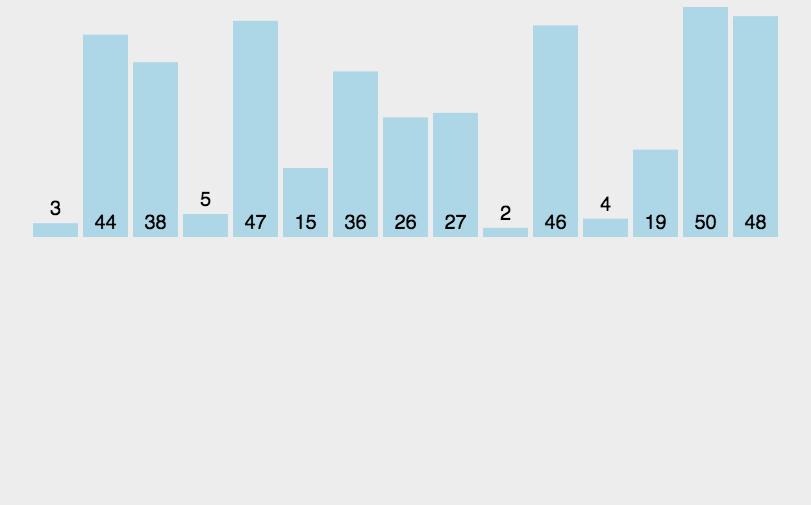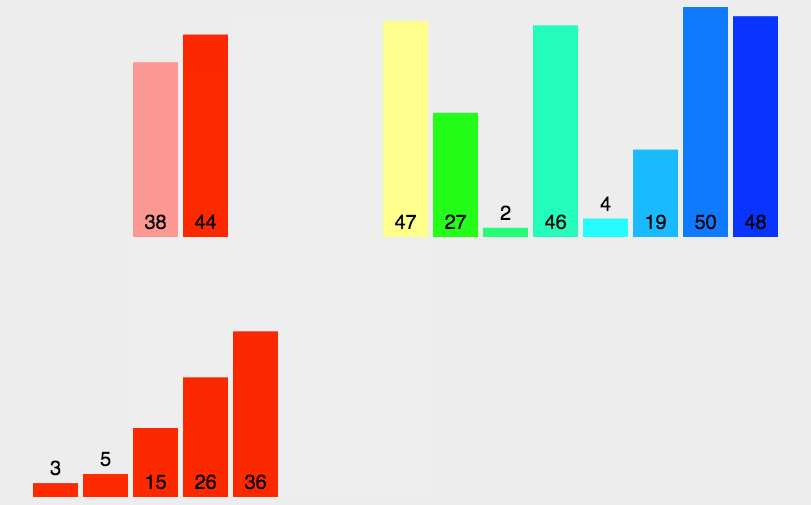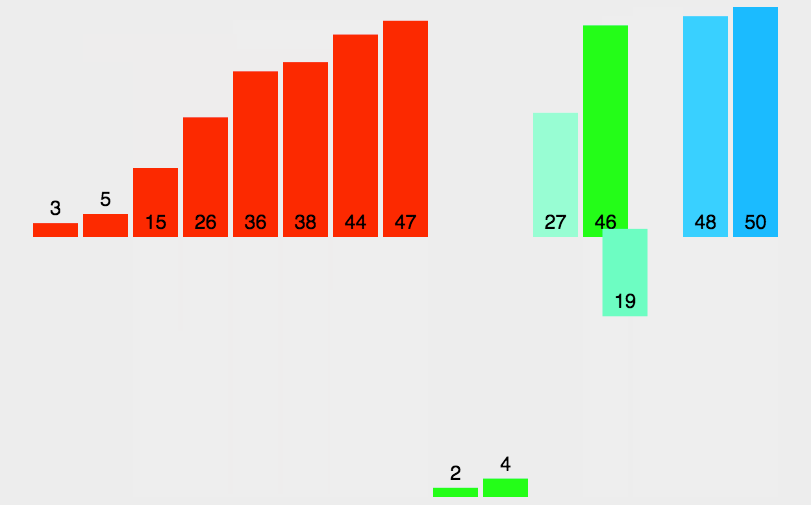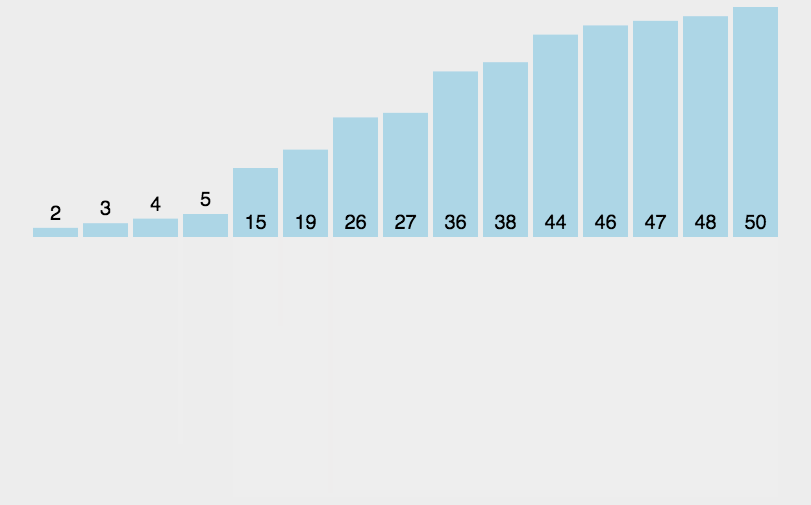
// MergeSort 归并排序函数
type MergeSort struct{}

// Sort 排序接口实现
func (ms MergeSort) Sort(arr []int) []int {
	if len(arr) <= 1 {
		return arr
	}

	mid := len(arr) / 2
	leftHalf := arr[:mid]
	rightHalf := arr[mid:]

	leftSorted := ms.Sort(leftHalf)
	rightSorted := ms.Sort(rightHalf)

	return merge(leftSorted, rightSorted)
}

// merge 合并两个已排序的切片
func merge(left, right []int) []int {
	result := make([]int, 0, len(left)+len(right))

	for len(left) > 0 && len(right) > 0 {
		if left[0] <= right[0] {
			result = append(result, left[0])
			left = left[1:]
		} else {
			result = append(result, right[0])
			right = right[1:]
		}
	}

	if len(left) > 0 {
		result = append(result, left...)
	} else if len(right) > 0 {
		result = append(result, right...)
	}

	return result
}

6希尔排序

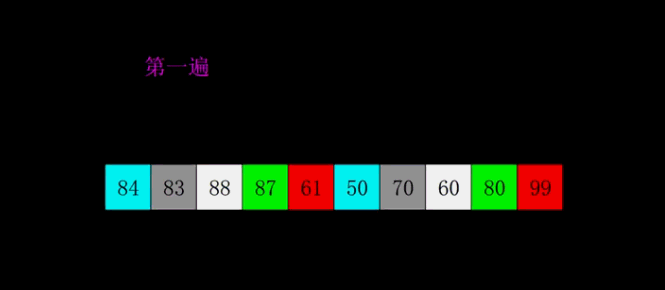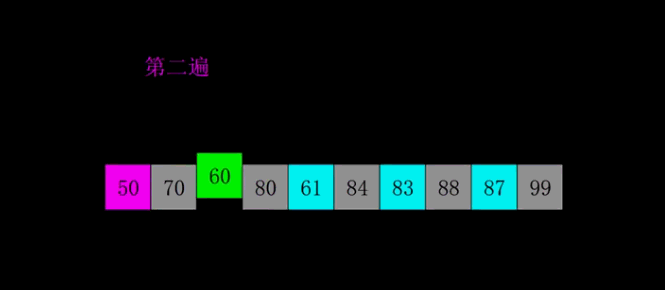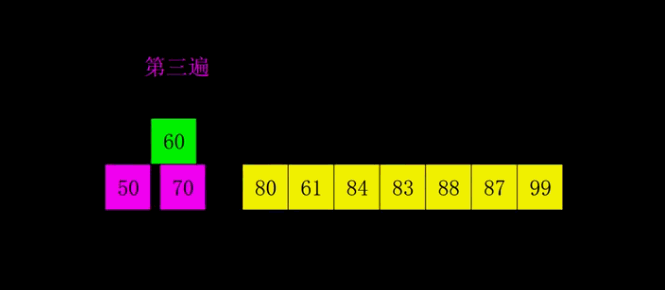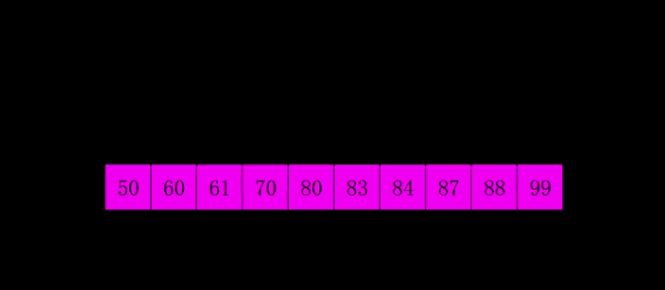
7.堆排序

8.计数排序

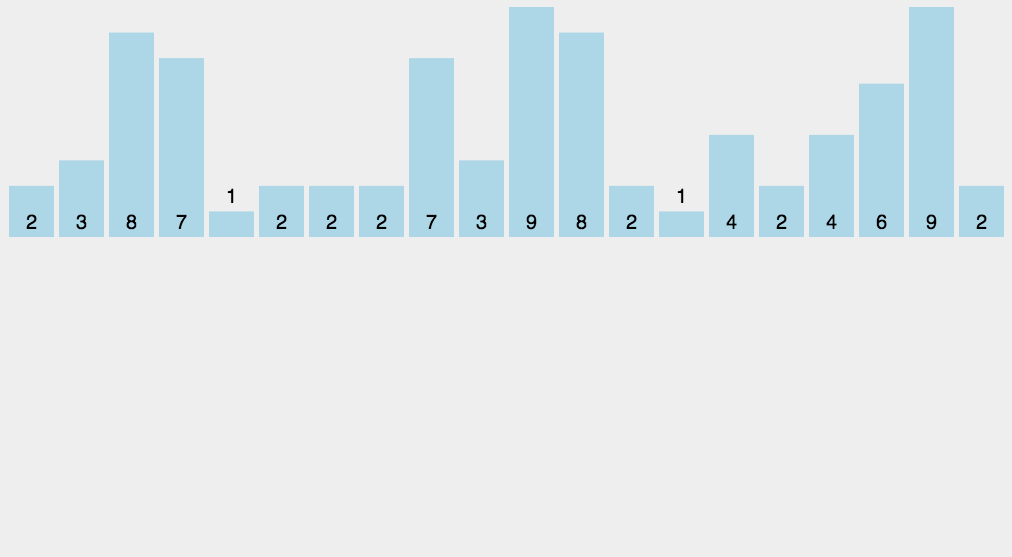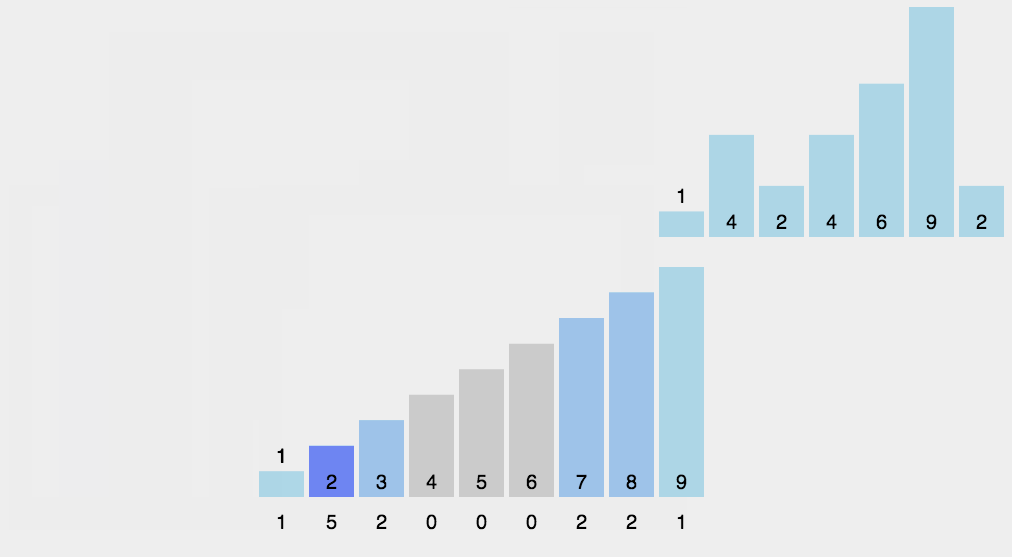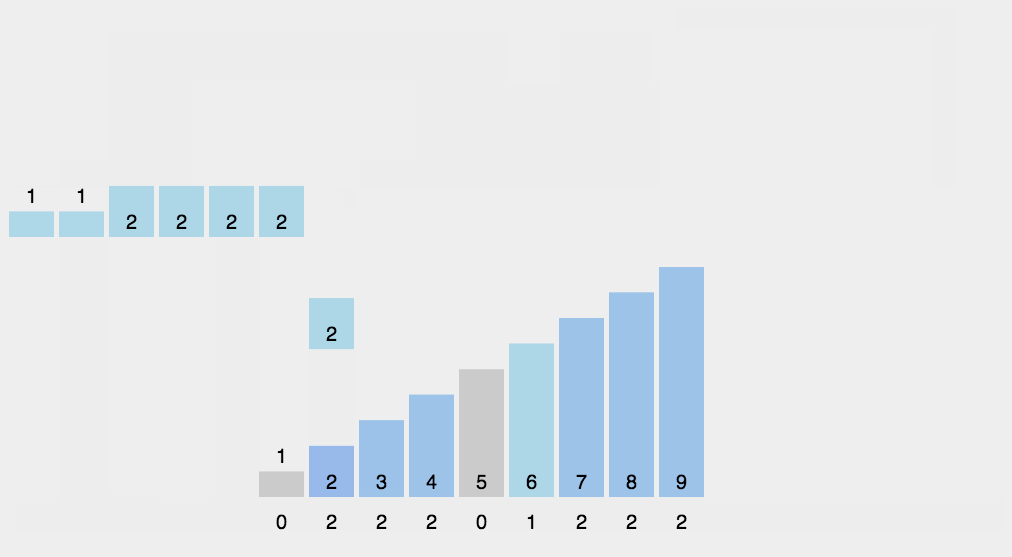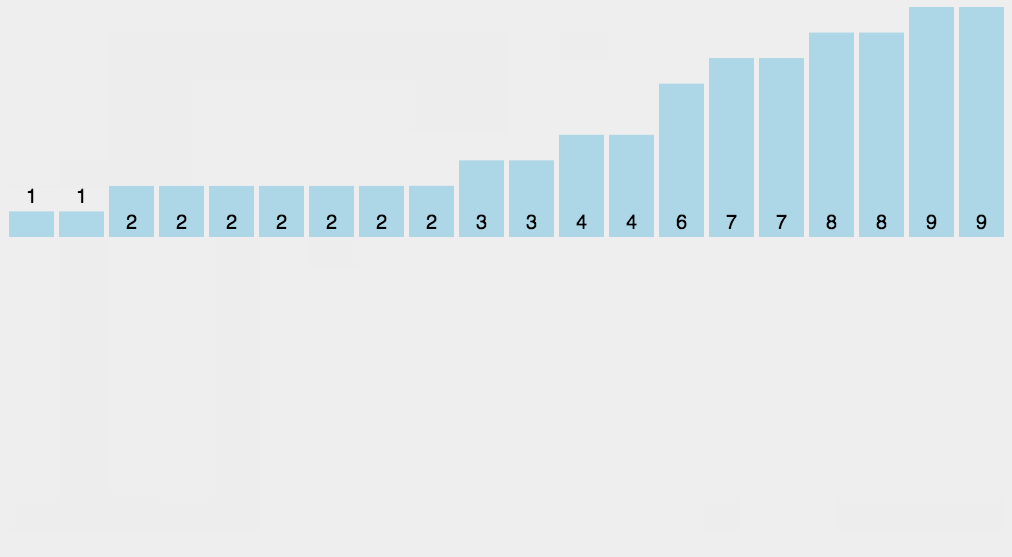
最后更新于 March 24, 2024

动态规划